Optimizing code execution speed – AV1 codec example

By: Segiy Sergienko, 23 Jan 2018

5 minutes

Reading Time: 5 minutes

All programs should work correctly; moreover, if you work with large data streams in real time, they should be really fast! To get maximum performance, the programmer should have strong platform architecture knowledge, including how it works at a low level. Since the beginning of 2000, vendors started to propose using a special command set (vector extensions) for similar operations on a data stream to get maximum speed from your processor. In addition, modern CPUs have separate registers for quick simple operations like multiplication, addition, copying, or permutation.

Let’s look inside an easy but real example: the high-resolution video encoding/decoding process. With incoming 2k and 4k standards becoming the norm, modern processing systems must be sufficiently optimized to deal with these.

For our research, we chose a real-life task – improving the speed of an open source AV1 codec using vector extensions and comparing the performance increase results.

The first step: we have to determine where to apply optimizations. To speed up your code, find the most critical parts of the current code in current conditions.

After this, we were able to identify things called hotspots – places that are executed most often in certain conditions. Then, for each hotspot we have to:

analyze the hotspot for optimization
optimize it (using AVX, in this particular case)
check that its behavior did not change.

Here is a C implementation of a function that computes the similarity of two 8×8 blocks by computing the mean square error:

uint64_t mse_8x8_16bit_c(uint16_t *dst, int dstride, uint16_t *src, int sstride)

{

uint64_t sum = 0;

int i, j;

for (i = 0; i < 8; i++) {

for (j = 0; j < 8; j++) {

int e = dst[i * dstride + j] – src[i * sstride + j];

sum += e * e;

}

return sum;

}

Let’s say that our hotspot is here, and the task is to optimize it using modern solutions like AVX/AVX2 CPU vector extensions.

We can observe that:

Rows of the 8×8 areas are contiguous in memory, so we can load them together.
Deltas are computed for each pair of pixels independently.
The sum of integers is an associative operation on any Intel/AMD CPU, so we can add the squares in the order we want.

What AVX/AVX2 instructions can offer us:

Addition and subtraction of eight 32-bit integers or sixteen 16-bit integers at once.
Multiplication is a bit trickier here. According to available instructions, you can perform multiplication of 16-bit and 32-bit integers in the same way as you do in scalar code. Also, you can multiply 32-bit numbers and store the result in 64 bits if it does not fit into 32 bits. But there’s no instruction to multiply pairs of 64-bits numbers in AVX2. Note that this is valid only if we’re completely sure what we’re doing.
Some stuff for loading and storing data from:
1. Aligned memory. In the case of AVX2, pointers should be aligned to 16 bytes;
2. Unaligned memory. This is slower than loading from aligned memory due to how the CPU handles memory.

So, what can we do?

Load the rows into eight separate registers (you may say, “Why? We can fit this in four registers,” and generally you will be right. But there’s a caveat in this particular case). This applies for both first and second regions.
And now we must pay attention. Look at this line:
int e = dst[i * dstride + j] – src[i * sstride + j];dst and src are uint16_t pointers. But the calculation is done in 32 bits, not 16. So, we have to convert uint16_t to int32_t. And yes, we have an AVX2 function for that. That is what I was talking about in the previous step. Initially, our row is 128 bits, occupying only half of the 256-bit register. When we convert uint16_t to int32_t, it will double in size and clearly will fit in the register.
After converting this, we can easily compute our differences. But here’s caveat #2. When simply taking the square of differences that are in int32_t and storing the result in int32_t, we will experience integer overflow when the input value is larger than sqrt(2^32-1). So, we should store these in int64_t. But that obviously means that we will multiply only half of the register. So, we have to take squares for each half independently.
After taking all squares, we can use mm256_add_epi64 to compute the result.
Our final result is a horizontal (per-element) sum of our final register.

One other example of the usage of vector extensions – the permutation of matrix elements: to change the placement of a 64-element matrix (32 bits each) in a special sequence (this is one of the stages of the discrete cosine transform implementation):

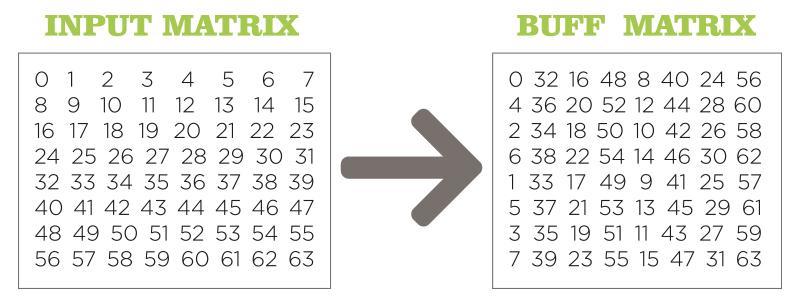
Each of the columns is permuted in the same way.

To prove this, you can just subtract the upper number from the corresponding column. You should get 0 4 2 6 1 5 3 7 everywhere. And because we are only working with rows, we should do the permutation first, and then transpose the matrix. So, using this approach, the 64 scalar instructions

bf1[0] = input[0];

bf1[1] = input[32];

…

bf1[62] = input[31];

bf1[63] = input[63];

fit into eight simple vector instructions, despite the fact that they don’t have any math here.

The effectiveness of these transformations and their impact on productivity depends on:

the algorithm that we rewrite using AVX instructions;
the frequency of interleaving vector instructions with scalar code.

Per-function experiments showed a speedup from 1.5x for the hardest cases to 8–11x in the best cases. Time was measured using std::chrono.

Let’s look more broadly at the example we started with: that AV1-like encoder with a very slow encoding process. It already has SSE implementations of various signal processing functions like convolutions, filters, discrete sine transforms, discrete cosine transforms, quantizations, etc.

It was analyzed for hotspots, and the most significant parts were implemented using AVX.

Then, we performed speed tests on streams of 240p, 480p, 720p, and 1080p.

The videos were tested on different encoder presets, which involved different mechanisms and hence different CPU usage and function usage. So, to have at least some speedup here, we have to identify the most common functions and rewrite them.

After rewriting, we noticed the following speedups:

240p: 1%–5% depending on mode. As this is the lowest resolution, the DSP routines take a small amount of time relative to other things.
480p: Similar to the previous case; up to 7% sometimes.
720p: 5%–15% depending on mode. Speedup increased as DSP became more important in terms of time.
1080p: Very similar to 720p.

Also, we should consider that we can highlight three broad classes of algorithms which can be used with AVX/AVX2 instructions:

those that work perfectly with extensions with minimum code changes required;
those that work well with extensions, but require many more code changes;
those poorly optimized for using AVX/AVX2 instructions; these may require extreme changes, even up to a full rebuild.

Even in the third case, code rewriting may make sense, especially if the data changes sequentially, or between parts that are already implemented using AVX2 (to decrease switching frequency between AVX and non-AVX mode).

Some notes about multi-core/parallel calculation:

Using normal multicore CPUs fully will lead to rewriting the whole codec at once – followed by heavy debugging!
Also, we don’t use GPUs for the following reasons:

1. see the first point above;

2. we have the penalty for transferring the data to and from the GPU;

3. some parts can’t be rewritten in a fully parallel way.

Contact us for more information and effective setup. You can tell us about your project details and we will help you to find the best solution to achieve your business goals.